Внедрение WMS

Как запустить современный складской комплекс благодаря цифровым технологиям и дискретной математике

Все больше предприятий автоматизируют свои складские комплексы на базе современных WMS (Warehouse Management System) в России. Внедрение WMS обеспечивает оптимизацию всех складских операций – приемка, размещение, хранение, отгрузка и другое, а также контроль работы персонала, складского оборудования и техники. Возможность управлять складскими процессами дает серьезное преимущество, позволяющее сократить до 40% затраты и издержки на содержание склада, сократить издержки, связанных с пересортицей товара на складе до 99.9%, повысить точность данных об остатках товаров и их местоположении до 99.9%, до 30% повысить оборачиваемость склада при тех же складских площадях, сократить количество персонала при сохранении объемов товарооборота до 20%.

Внедрение WMS: кейс компании LD

Компания LD – крупнейший в России производитель стальных цельносварных шаровых кранов, выпускаемых с 2003 г. Шаровые краны LD предназначены для монтажа в трубопроводах, предназначенных для транспортировки нефти и газа, системах тепловодоснабжения, технологических трубопроводах, различных агрегатах. Сегодня мощность склада составляет 3-5 тысяч паллет в месяц, складские площади – 3025 кв.м. (хранение 5-7 ярусов).

На протяжении многих лет в компании LD существовала проблема, связанная с недостатком складских площадей. Что не позволяло эффективно выстроить складские процессы, не соответствовало объему производства, не обеспечивало рост объёмов производства и продаж. Склады были разрознены территориально и располагались рядом с производственными площадками и цехами.

Для решения проблемы недостатка складских площадей был спроектирован и построен новый складской комплекс, оснащенный необходимым стеллажным оборудованием и техникой. Для того, чтобы эффективно выстроить и автоматизировать складские процессы, руководство компании обратилось в компанию Первый Бит. Эксперты Первого Бита предложили решение – внедрение WMS-системы «1С:Предприятие 8. 1С-Логистика:Управление складом», выступили поставщиком цифровых технологий для складской логистики LD и интегратором программно-аппаратного комплекса на базе WMS-системы с корпоративной информационной системой заказчика.

Перед специалистами Первого Бита была поставлена задача выполнить проект автоматизации складской логистики в период низкого сезона с августа по ноябрь. Клиенты компании LD – это предприятия жилищно-коммунального хозяйства, а также компании, отвечающие за монтаж, модернизацию и ремонт трубопроводов, где используются шаровые краны LD. В зимнее время производитель начинает принимать заказы и заполнять склад готовой продукцией, где она хранится в соответствующих условиях до момента отгрузки, как правило, ближе к летнему сезону. Поэтому календарный план проекта был подчинён сезонности в деятельности компании-заказчика. Важным было уложиться точно в срок и выполнить весь цикл работ:

• проектирование WMS-системы,
• разработка, настройка и тестирование системы,
• запуск системы в промышленную эксплуатацию, включая обучение сотрудников складского комплекса, отдела логистики и производственных участков.

Проект автоматизации выполнялся параллельно со строительством и оснащением нового складского комплекса. По готовности инфраструктуры складского комплекса к приёму продукции LD и без остановки деятельности был выполнен переезд и освобождение старых складских площадей. Успешность проекта обусловлена слаженностью и синхронностью работы совместной команды интегратора и заказчика. Благодаря такому сотрудничеству запуск нового склада выполнен с минимальным отклонением от установленных сроков – менее месяца.

Успешность проекта обусловлена соединением промышленной разработки и научного подхода в использовании цифровых технологий – разработаны и внедрены интеллектуальные алгоритмы оптимизации, которые:

• значительно упростили работу операторам WMS-системы,
• сэкономили время кладовщиков при выполнении складских операций
• и обеспечили максимальное использование складских мощностей.

Основным критерием применимости таких интеллектуальных алгоритмов было условие: алгоритм должен предлагать решение, как минимум, не хуже, чем способен дать оператор WMS с большим опытом и полным знанием специфики складских процессов компании-заказчика. При этом, алгоритм выдаёт моментальное решение, а оператору WMS требуется на поиск рабочего варианта решения 20-30 секунд. В масштабах складского комплекса эффективность составляет часы. Алгоритмы оптимизации разработаны на языке C++ и подключены к базе данных WMS-системы как внешние компоненты.

При разработке алгоритма специалисты опирались на исследования, описанные в ряде научных математических работ, как отечественных, так и зарубежных. Разработанный алгоритм сжатия используют такие известные математические алгоритмы:

• алгоритм динамического программирования: для решения задачи о рюкзаке;
• жадный рандомизированный алгоритм: для решения задачи о покрытии множествами (для кластеризации партий);
• алгоритм локальный поиск: для улучшения имеющегося сжатия;
• алгоритм решения транспортной задачи (задача Канторовича-Монжа): для формирования начального назначения остатков в ячейки сжатия.

В настоящее время такая обработка используется систематически, и операторы WMS подтверждают хорошее качество кластеризации партий и компактности размещений.

Также в ходе проекта были автоматизированные следующие процессы:

1. Автоматическая генерация штрих-кодов и печать этикеток на принимаемую продукцию от производства.
2. Приемка товара с помощью терминала сбора данных.
3. Размещение товара с помощью терминала сбора данных. Была решена задача оптимального планирования размещения товаров разных габаритов в ячейки различной вместимости.
4. Подпитка с помощью терминала сбора данных.
5. Отбор товара с помощью терминала сбора данных. Разработан функционал отбора составных грузов на ТСД с учетом специального порядка и рядности размещения товаров на поддоне.
6. Отгрузка товаров с помощью ТСД. Отгрузка по схеме кросс-докинг.
7. Внутреннее перемещение с помощью ТСД.
8. Инвентаризация остатков товаров на складе с помощью ТСД.
9. Операция оптимального сжатия остатков товаров в ячейках с целью увеличения плотности хранения остатков и увеличение количества свободных ячеек.

WMS-система интегрирована с корпоративной информационной системой на базе 1С:Управление торговлей 10.3 и 1С:Управление производственным предприятием. В дальнейшем LD рассматривает переход на современное промышленное решение «1С:ERP Управление предприятием 2».

Сейчас WMS-система поддерживается специалистами Первого Бита и продолжает развиваться за счет разработки и реализации алгоритмов оптимизации складских процессов, которые позволят улучшить их точность и повысить качество, используя текущую мощность складского комплекса, оптимизируя логистические процессы.

Дискретная математика при внедрении WMS на складе

Узкое место в процессах

При проектировании схем автоматизации складских процессов мы столкнулись с существующей проблемой неоптимального хранения запасов. Специфика хранения и укладки кранов такая, что в одной ячейке штучного хранения может находиться только номенклатура одной партии. Продукция приходит на склад ежедневно и каждый приход – это отдельная партия. Итого, в результате 1 месяца работы склада создаются 30 отдельных партий, притом, что каждая должна хранится в отдельной ячейке. Товар зачастую отбирается не целыми палетами, а штуками, и в результате в зоне штучного отбора во многих ячейках наблюдается такая картина: в ячейке объемом более 1м3 лежит несколько штук кранов, которые занимают менее 5-10% от объема ячейки.

Рис 1. Фото нескольких штук в ячейке

На лицо неоптимальное использование складских мощностей. Чтобы представить масштаб бедствия могу привести цифры: в среднем таких ячеек объемом более 1м3 с «мизерными» остатками в разные периоды работы склада насчитывается от 100 до 300 ячеек. Так как склад относительно небольшой, то в сезоны загрузки склада этот фактор становится «узким горлышком» с сильно тормозит складские процессы.

Идея решения проблемы

Возникла идея: партии остатков с наиболее близкими датами приводить к одной единой партии и такие остатки с унифицированной партией размещать компактно вместе в одной ячейке, или в нескольких, если места в одной не будет хватать на размещение всего количества остатков.

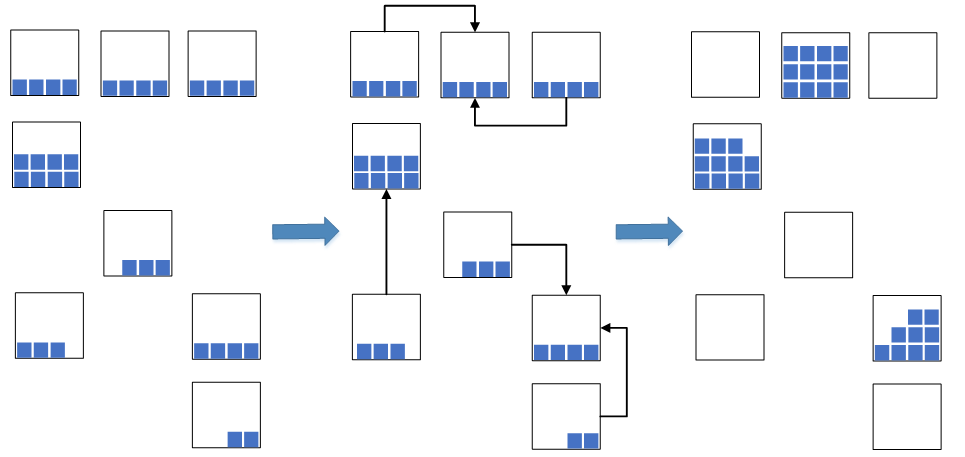
Рис.2. Схема сжатия остатков в ячейках

Это позволяет значительно сократить занимаемые складские площади, которые будут использоваться под новый размещаемый товар. В ситуации с перегрузкой складских мощностей такая мера является крайне необходимой, в противном случае свободного места под размещение нового товара может попросту не хватить, что приведет к стопору складских процессов размещения и подпитки. Раньше до внедрения WMS такую операцию выполняли вручную, что было не эффективно, так как процесс поиска подходящих остатков в ячейках был достаточно долгим. Сейчас с внедрением WMS решили процесс автоматизировать, ускорить и сделать его интеллектуальным.
Процесс решения такой задачи разбивается на 2 этапа: на первом этапе мы находим близкие по дате группы партий для сжатия, на втором этапе мы для каждой группы партий вычисляем максимально компактное размещение остатков товара в ячейках. Остановимся на первом этапе алгоритма, а освещение второго этапа оставим для следующей статьи.

Поиск математической модели задачи

Перед тем как садиться писать код и изобретать свой велосипед, мы решили подойти к такой задаче научно, а именно: сформулировать ее математически, свести к известной задаче дискретной оптимизации и использовать эффективные существующие алгоритмы для ее решения или взять эти существующие алгоритмы за основу и модифицировать их под специфику решаемой практической задачи.

Так как из бизнес-постановки задачи явно следует, что мы имеем дело с множествами, то сформулируем такую задачу в терминах теории множеств. Пусть P – множество всех партий остатков некоторого товара на складе. Пусть С – заданная константа дней. Пусть K – подмножество партий, где разница дат для всех пар партий подмножества не превосходит константы C. Требуется найти минимальное количество непересекающихся подмножеств K, такое что все подмножества K в совокупности давали бы множество P.
Иными словами, нам нужно найти группы или кластеры схожих партий, где критерий схожести определяется константой C. Такая задача напоминает нам хорошо известную всем задачу кластеризации. Важно сказать, что рассматриваемая задача отличается от задачи кластеризации, тем что в нашей задаче есть жестко заданное условие по критерию схожести элементов кластера, определяемое константой C, а в задаче кластеризации такое условие отсутствует.

Итак, нам удалось сформулировать задачу и найти классическую задачу с похожей постановкой. Теперь необходимо рассмотреть общеизвестные алгоритмы для ее решения, чтобы не изобретать велосипед заново, а взять лучшие практики и применить их. Для решения задачи кластеризации мы рассматривали самые популярные алгоритмы, а именно: k-means, c-means, алгоритм выделения связных компонент, алгоритм минимального остовного дерева.

Для решения нашей задачи алгоритмы кластеризации k-means и c-means не применимы вовсе, так как заранее никогда не известно количество кластеров k и такие алгоритмы не учитывают ограничение константы дней. Такие алгоритмы были изначально отброшены из рассмотрения.

Для решения нашей задачи алгоритм выделения связных компонент и алгоритм минимального остовного дерева подходят больше, но, как оказалось, их нельзя применить «в лоб» к решаемой задаче и получить хорошее решение. Чтобы пояснить это, рассмотрим логику работы таких алгоритмов применительно к нашей задаче.
Рассмотрим граф G, в котором вершины – это множество партий P, а ребро между вершинами p1 и p2 имеет вес равный разнице дней между партиями p1 и p2.
В алгоритме выделения связных компонент задается входной параметр R, где R <= С, и в графе G удаляются все ребра, для которых вес больше R. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение R, при котором граф «развалится» на несколько связных компонент, где партии, принадлежащие этим компонентам, будут удовлетворять нашему критерию схожести, определяемому константой C. Полученные компоненты и есть кластеры.

Алгоритм минимального покрывающего дерева сначала строит на графе G минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом до тех пор, пока граф не «развалится» на несколько связных компонент, где партии, принадлежащие этим компонентам, будут также удовлетворять нашему критерию схожести. Полученные компоненты и будут кластерами. При использовании таких алгоритмов для решения рассматриваемой задачи может возникнуть ситуация как на рисунке 3.

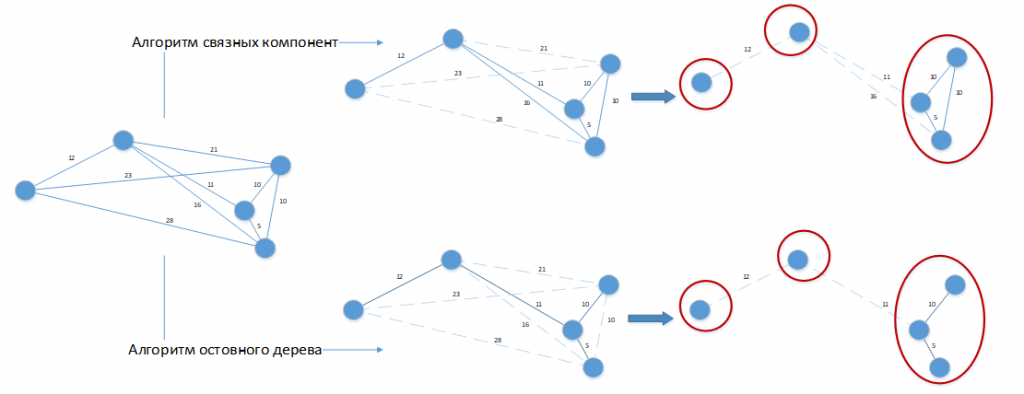
Рисунок 3. Применение алгоритмов кластеризации к решаемой задаче

Допустим, у нас константа разницы дней партий равна 20 дней. Граф G был изображен в пространственном виде для удобства визуального восприятия. Оба алгоритма дали решение с 3-мя кластерами, которое можно легко улучшить, объединив партии, помещенные в отдельные кластеры, между собой. Очевидно, что такие алгоритмы необходимо дорабатывать под специфику решаемой задачи и их применение в чистом виде к решению нашей задачи будет давать плохие результаты.

Итак, прежде чем начинать писать код модифицированных графовых алгоритмов и изобретать свой велосипед (в силуэтах которого уже угадывались очертания квадратных колес), мы, опять же, решили подойти к такой задаче научно, а именно: попробовать свести ее к другой задаче дискретной оптимизации, в надежде на то, что существующие алгоритмы для ее решения можно будет применить без модификаций.

Очередной поиск похожей классической задачи увенчался успехом. Удалось найти задачу дискретной оптимизации, постановка которой 1 в 1 совпадает с постановкой нашей задачи. Этой задачей оказалась задача о покрытии множествами. Приведем постановку задачи применительно к нашей специфике.

Имеется конечное множество P и семейство S всех его непересекающихся подмножеств партий, таких что разница дат для всех пар партий каждого подмножества I из семейства S не превосходит константы C. Покрытием называют семейство U наименьшей мощности, элементы которого принадлежат S, такое что объединение множеств I из семейства U должно давать множество всех партий P.

Алгоритм решения задачи

С математической моделью решаемой задачи определились. Теперь приступим к рассмотрению алгоритма для ее решения. Подмножества I из семейства S можно легко найти следующей процедурой.

1. Упорядочить партии из множества P в порядке убывания их дат.
2. Найти минимальную и максимальную даты партий.
3. Для каждого дня t от минимальной даты до максимальной найти все партии, даты которых отличаются от t не более чем на С/2 (поэтому значение C лучше брать четное). Логика работы процедуры формирования семейства множеств S при C = 20 дней представлена на рисунке 4.
4. 
   

Рисунок 4. Формирование подмножеств партий

В такой процедуре необязательно для каждого t перебирать все другие партии и проверять разность их дат, а можно от текущего значения t двигаться влево или право до тех пор, пока не нашли партию, дата которой отличается от t более чем на половинное значение константы. Все последующие элементы при движении как вправо, так и влево будут нам не интересны, так как для них различие в днях будет только увеличиваться, поскольку элементы в массиве были изначально упорядочены. Такой подход будет существенно экономить время, когда число партий и разброс их дат значительно большие. Для решения задачи о покрытии множествами был выбран жадный алгоритм, который показывает неплохие результаты в качестве решения для задач небольшой размерности, достаточно прост в реализации и быстр, так как оценка его времени работы равна O(mn). Жадный алгоритм выбирает множества руководствуясь следующим правилом: на каждом этапе выбирается множество, покрывающее максимальное число ещё не покрытых элементов. Подробное описание алгоритма и его псевдокод можно найти здесь (ссылка).
Сравнение точности такого жадного алгоритма на тестовых данных решаемой задачи с другими известными алгоритмами, такими как вероятностный жадный алгоритм, алгоритм муравьиной колонии и т.д., не производилось.

Реализация алгоритма «кластеризации» в обработке 1С

Такой алгоритм для решения первой задачи кластеризации партий был реализован на языке 1С и был включен во внешнюю обработку под названием «Сжатие остатков», которая была подключена к WMS-системе. Мы не стали реализовывать алгоритм на языке С++ и использовать его из внешней компоненты, что было бы правильней, так как скорость работы кода на C++ в разы и на некоторых примерах даже в десятки раз превосходит скорость работы аналогичного кода на 1С. На языке 1С алгоритм был реализован для экономии времени на разработку и простоты отладки на рабочей базе. Результат работы алгоритма представлен на рисунке ниже.

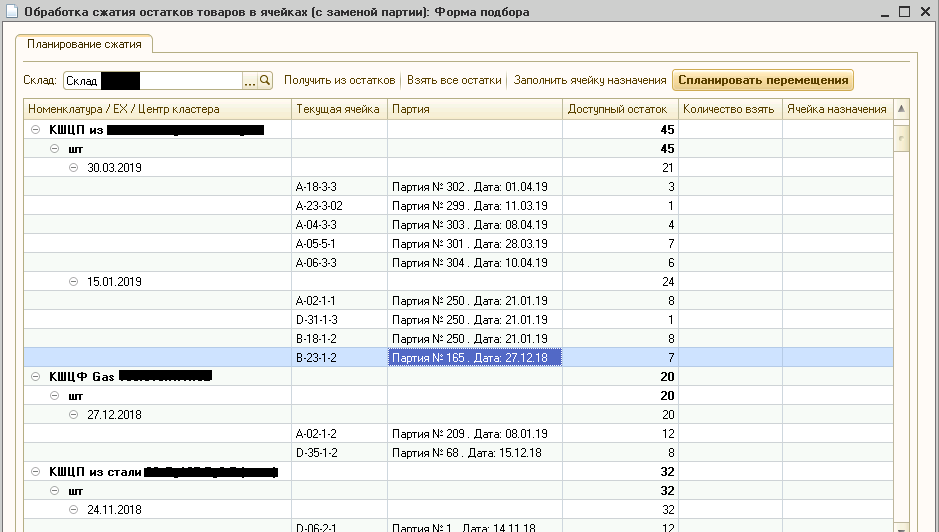
Рис.5. Обработка по «сжатию» остатков

Отметим, что в настоящее время такая обработка используется в продакшене систематически, и операторы WMS подтверждают хорошее качество кластеризации партий. Описание алгоритма оптимального сжатия, которому на вход подается массивы кластеризованных партий, рассмотрим позднее.

Внедрение WMS. Выводы

Главный опыт, который мы получили от решения такой практической задачи – это подтверждение эффективности использования парадигмы: математическая формулировка задачи - известная математическая модель - существующий алгоритм. Дискретной оптимизации уже насчитывается более 300 лет и за это время люди успели рассмотреть очень много задач и накопить большой опыт по их решению. В первую очередь, целесообразнее обратиться к этому опыту, а уже потом начинать изобретать свой велосипед.

Еще один факт с которым мы столкнулись это то что на многих предприятиях есть потребности в решении различных задач оптимизации, причем их решение может принести существенный эффект: сократить издержки, экономить время, устранить узкие места в процессах. Но зачастую они так и остаются потребностями и проблемами, так как ни руководство, ни сотрудники не знакомы с подходами к решению таких задач и не знают, что такие задачи могут быть эффективно решены с помощью методов оптимизации.

Безусловно, большинство задач оптимизации операций возможно решать только при хорошо налаженной работе информационной системы, в данном случае WMS-системы, поскольку оптимизация без предварительной информатизации малополезна, так как не откуда брать данные и некуда данные решения алгоритма записывать. Конечно, сейчас мы не говорим о ситуациях, когда нужно один раз и на долгое время найти оптимальный вариант работы какого-либо процесса, например, найти оптимальную конфигурацию и оптимальные параметры цепочки поставок, хотя даже и в таких задачах наличие исторических данных из корпоративной учетной системы будет неоспоримо полезно. Поэтому мы, команда Первого Бита, практикуем после внедрения информационной системы, будь то «1С:Предприятие 8. 1С-Логистика:Управление складом», «1С:ERP», «1С:Управление торговлей» и другие, делать небольшие дополнительные проекты по оптимизации тех процессов, которые выявились в ходе внедрения информационной системы как проблемные и важные для клиента. Думаю, это перспективная практика, которая в последующие годы будет набирать обороты.